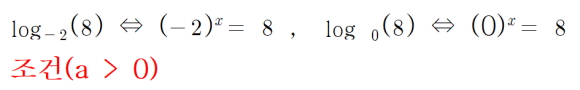027. 대수(log)는 원래의 “거리” 계산 툴 지수이고 그 2) 거리는 음수가 없으며 실수의 0 제곱은 1이다.
[김선생님s’ 수학 클리닉] = 로그(log)와 지수법칙은 분리할 수 없는 관계를 갖고 있으나 많은 학생들이 지수법칙을 제대로 이해하지 못하고 있어 로그(log)에 대해서도 많은 것을 어렵게 만든다.
대수 천문학 항해술 등 대규모 숫자 계산에 활용 고교 과정에서의 대수는 천문학 항해술 등의 거리(숫자 크기가 엄청난 것이었다) 계산을 용이하게 하기 위한 것이라고 생각하면 큰 무리가 아닐 것이다. 그 연원은 컴퓨터와 계산기가 없던 17세기에 네이피아가 고안(또는 발견한)해 복잡한 계산(특히 곱셈)에 위력을 발휘했다.
②그 장점은 곱셈을 덧셈으로 바꾸어 계산하는 것이다. 계산기가 있는 현대와 달리 17~18세기에 여섯 자리 이상의 숫자를 2~3번 걸면 대부분의 수학자는 피곤해지기 일쑤였다.
123456×4567890———???????????
③지구의 공전궤도를 발견해 케플러 법칙을 수립한 케플러의 스승 타코 브라헤가 바로 삼각함수를 활용해 복잡한 계산을 쉽게 해낸 수재 중의 하나였다. 천문학자 타코 브라헤가 지구와 태양과의 거리, 지구와 달의 거리, 지구와 화성과의 거리를 계산하느라 고생했음을 상상하며 즐거운 마음으로 로그의 기본만이라도 배워보자.
2) 로그 아래는 0보다 큰 1이 아니라 수 ① 먼저 로그의 정의를 보면
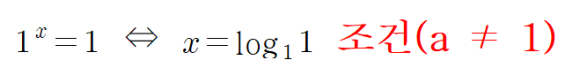
라고 대부분의 교과서와 참고 자료는 소개한다. 여기에 하나를 더하면 한번 깔린 수(a)는 특별한 경우가 아니면 항상 ‘아래’에서 벗어날 수 없다. a, b, 는 모두 양수여야 한다. 단, a는 1이 될 수 없다. x는 틀리면 다 된다.
②일단 정의부터 로그는 지수의 또 다른 표현 방법이라는 것을 알 수 있다. 또 거리 계산을 위한 도구라는 것도 설명했다.따라서, 깔리는 수 「a」는 0보다 작은 것은 있을 수 없다(거리이므로). 0이면 의미가 없다(거리가 0이면~). 게다가 소수점 크기(0.1)라도 상관없다(역시 거리의 크기이므로).
③그러나 1의 경우는 수학적으로 큰 의미가 없다. ‘1’은 어떠한 제곱을 해도 1이 된다. 심지어 1에는 0제곱을 해도 1이 된다(지수법칙으로 설명했다. 014. 참조).
④ 양수를 제곱(홀수 번이든 짝수 번이든)하면, 그 연산 결과는 당연히 양수이므로 정수 ‘b’는 0보다 크다.
⑤이 설명에는 로그는 실수의 범위에서만 성립하는 것을 전제로 하고 있다. 실수는 수직선상에 존재하는 수이며, 무리수여도 상관없다. 또한 수직선 두 개를 섞어 만든 좌표 평면에도 존재하므로 각종 함수와 그래프로 나타낼 수도 있다.
3) 대수 밑과 진수 조건에 대한 잔소리 수준의 설명이 구체적 숫자로 아래 ‘a’와 진수 ‘b’에 대해 조건(a:1, a > 0, 진수 b > 0)에 반하는 경우를 가정해 보자. 원래의 대수는 지수법칙으로부터 생겨난 것이므로 지수법칙과 관련하여 생각해 보자.
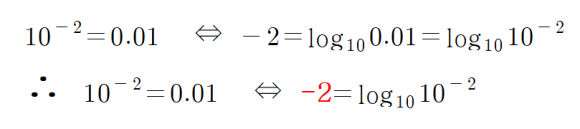
①1은 무수히 겹쳐 제곱을 해도 항상 1이 되므로, x를 만족하는 해, 정답이 무수히 많은(부정) 것을 알 수 있다.

②1은 어떤 수를 제곱해도 1이므로 x를 만족하는 해, 정답은 없다(불능). 따라서 수학적으로 무의미하다.

③ 본래의 지수법칙에서 x는 실수이므로 양의 정수 ‘2’에 어떤 실수를 제곱해도 절대로 0보다 작아질 수 없다.따라서, 위의 식 좌변과 우변은 모두 수학적으로 정의되어 있지 않은 것(무의미)이다.
④더 나아가라.
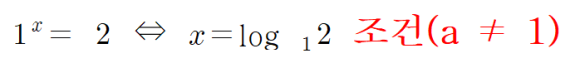
등도 원래의 대수를 나타내도록 한 지수법칙과 관련하여 생각하면 어느 것도 무의미하다.
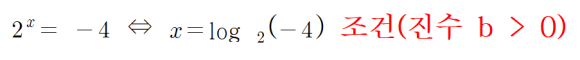
와 같은 성립조건은 (x-2 )이 0이 아니면 (전체를 제곱하므로) x-2일 뿐으로 성립한다.
⑤그렇다면, a=10, x=-2, b=0.01의 경우를 살펴보자.
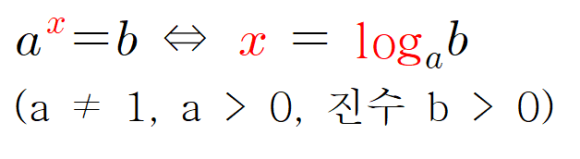
상기와 같이 성립한다.
예로 확인해 보자.