
만나서 반갑습니다EDU입니다! 오늘은 지난 시간에 전해드린 루트 계산법 후속편! 루트 나눗셈 하는 법을 공부하겠습니다.
지난 시간! 잊으신 건 아니죠? ROOT 문제를 풀 때는 규칙도 중요하지만 최종 계산된 값을 제곱근의 개념!으로 표현하는 것! 인지하고 있어야 합니다:)
그럼 바쁘실 텐데, 바로 본론으로 들어가서 루트에서 나눗셈을 찾을 때는 어떤 원리로 풀어야 하는지 같이 살펴보겠습니다.
먼저 보통 쓰는 숫자 기준! 즉 자연수 기준으로 나눌 때 어떤 원리였는지 기억을 더듬어야 합니다.
2 나누기 3 = ? 이런 문제를 풀 때 독자는 어떻게 했을까요?:)
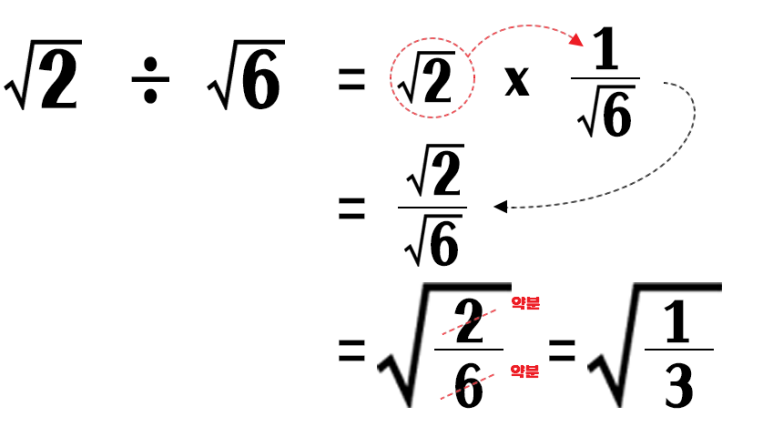
답은 분수로 표현할 때도 있고 무한소수로 계산하는 표시법도 있어요. 그리고 루트 값과 자연수의 숫자를 나누는 계산도 있는 것이군요.
이 개념을 그대로 루트(ROOT) 나눗셈으로 옮겨서 써보는 건데요? 기본 사칙연산 규칙은 이미 아실 테고 언급했듯이 다른 가격과 계산하는 순간이 있으니까! 오늘처럼 다른 콘텐츠를 만들게 되었습니다.
자,그럼본격적으로루트나누기계산문제를한번풀어보죠.
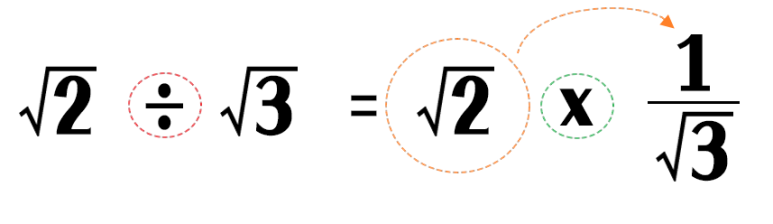
표시된 문제를 나눗셈해서 계산한다고 했을 때 어떻게 하면 좋을까요?
역수 개념을 적용하여 뒤에 표시된
그 뒤에 그냥 올리고 풀면 돼요.
따라서라고표기가되어도이대로마무리를하면안되죠?
답을 표기할 때!정확하게 -로 작성하는 것이 맞습니다.
너무 쉽죠?
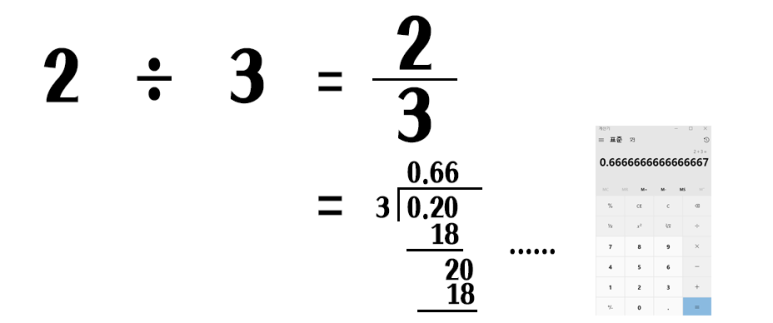
이번에는 조금 다른 문제를 풀어보겠습니다이번에는 ***입니다.
푸는 방법을 보면 아까 설명했듯이 분수로 표기할 수 있죠? 하지만 이번에는 ‘약분’이 되는 가격입니다.
그래서 그대로 계산해서 사용하지 않고 약분된 값을 쓰시면 됩니다.:)
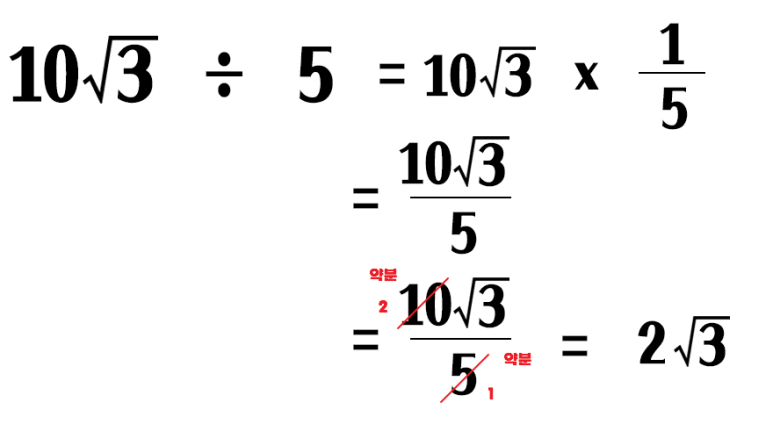
이번 문제는 응용편이에요 루트 값과 자연수의 값을 나눈다고 하면 어떻게 할까요?
원리는 앞에서 하던 것과 같아요.우선 역수로 나누는 것을 다시 걸어 주시고, 그렇다면…이군요? 그냥 분수 값에 올라간다는 거! 잘 풀렸나요?
그런데 10이라는 값과 5는 자연수이면서 동시에 약분이 됩니다. 따라서최종정답은!?이됩니다.

마지막 문제입니다.분수로 구성되어 있는 ROOT 값을 풀어보겠습니다
이럴 때는 대각선으로 약분된 값으로 계산해야 합니다. 처음에나누기를걸면역수개념을적용해서문제를풀어가는것은똑같습니다.
해설내용을보면어떻게푸는지이해할수있을거예요.
이전부터 오늘의 콘텐츠까지 루트 계산법에서 여러 개의 기본 내용 중 하나입니다.자신의 실력 향상을 생각한다면, 반드시 다른 유형의 공식도 풀어서 값을 구할 수 있어야 해요!
앞으로학습에필요한기본공식을정리하고알려드리는시간을갖겠습니다.그때도 오늘처럼 또 와주셨으면 좋겠습니다. ^_^
그럼 이만 소식을 마치도록 하겠습니다. 다음에 뵙겠습니다.감사합니다